Step 7: Solve Remaining Five Corners

Solve remaining corner cubies
by rotating them in place.

Basic Idea

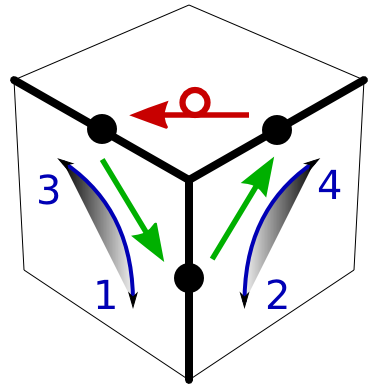
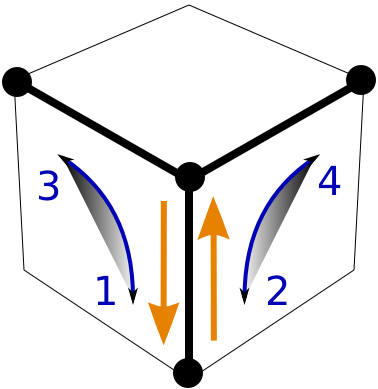
Use the upside-down Y-move twice to rotate corner cubies in place. The basic move that rotates two corner cubies but leaves all others unchanged is y y U yi yi Ui.

Details

We focus on the cubie at the top of the vertical column of the upside-down Y-move, which we denote as y-move. We do the y-move twice in sequence.

Doing y y rotates the up-front-right corner by 120 degrees counter-clockwise.
Doing yi yi rotates the up-front-right corner by 120 degrees clockwise.

Our strategy is as in Step 6. We have a move (the double y-move) that does what we want to exactly one corner cubie in the upper layer, but it creates a mess in the lower layers. We clean up by applying the inverse of the y-moves, but only after moving the U-layer.

Here are several examples:

Rotating corner cubie in place with double yi-move.

Use yi yi to rotate the yellow-green-orange corner cubie in place by 120 degrees in the clockwise direction. Note that the first R-move indicates the sense of rotation: the green facelet moves from the front into the top layer.

Rotating two corner cubies in place in opposite directions without side effects.

Use yy U yiyi Ui to first turn one corner cubie counter-clockwise and then a second corner cubie clockwise. This leaves the middle and bottom layer unchanged.

Sometimes we would like to turn three corner cubies clockwise. We can do this by applying yyUyiyiUi twice. We turn the first cubie clockwise, but then one of the others has to receive the counter-clockwise rotation, which is the opposite direction we wanted. However, we are then left with two cubies which need a clockwise and a counter-clockwise rotation, which the second yyUyiyiUi can handle. We have used 8 y-moves to do three clockwise rotations.

However, we can also do three clockwise rotations with just 6 y-moves. Recall that doing any Y-move six times gives us the identity (!). Just try it. Throw in some U-moves and we can rotate three corner cubies in the same direction:

Rotating three corner cubies in place in the same direction without side effects.

Use yy U yy U yy U2 to turn three corner cubies counter-clockwise. This leaves the middle and bottom layer unchanged.

Finally, it may happen that the green-orange-white corner in the bottom layer has to be rotated. We can solve this problem by turning the entire cube so that the g.o.w. cubie is in the top layer and applying the moves given above.

Comments

The moves introduced above are actually sufficient to undo all remaining rotations. A cubie can have one of three orientations, say rotated by 0, 120, or -120 degrees. However, the laws of the cube show that there cannot be a single cubie with a clockwise or counter-clockwise rotation in an otherwise completely solved cube. Essentially, all rotations have to add up to multiples of 360 degrees. The double y-move sequence discussed above is sufficient to undo all remaining rotations because it can handle all cases of rotations that add up to multiples of 360 degrees, and these are all the cases that the laws of the cube allow.

The final step orienting the corners is in some sense the least efficient one. Just consider the following: we need 27 elementary moves to rotate three corners in place, while the perfect solution to unscramble an entire cube needs at most 20 moves!

Alternatives

Recall the move LDDLi used to position the corner cubies in the previous step. The Wikibook-2008 solution uses this move combined with the analogous move FiDDF to orient cubies as well: LDDLi FiDDF turns the up-front-left corner cubie counter-clockwise, but leaves some cubies scrambled. FiDDF LDDLi turns this cubie clockwise and undoes the scrambling. Combine with U-turns as in our y-move sequence.