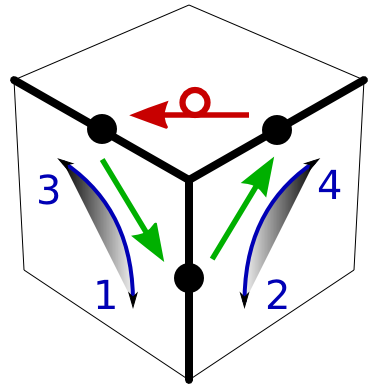
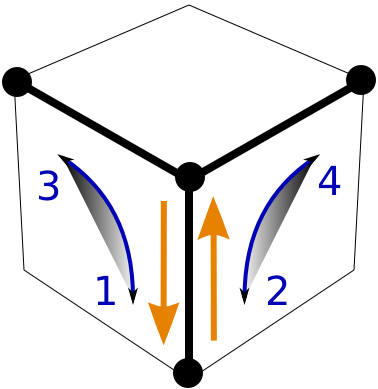
A Beginner's Method
to Solve The Cube
Basics
Solving the Cube
- Step 1: Bottom Edges
- Step 2: Bottom Corners
- Step 3: Middle Edges
- Step 4: Top Edges
- Step 5: Solve Edges
- Step 6: Position Corners
- Step 7: Solve Corners
- Done
Extras
Step 5: Solve Last Three Edges
| Solve the last 3 edge cubies. |
|
Basic Idea
Combine Y-moves with U-moves to solve the remaining three edge cubies.
We choose to solve the green-orange cubie first and see what happens to the remaining two cubies in the top layer.
Details
The tricky bit is that any Y-move will affect three edge cubies simultaneously. There are three cases to consider, and they depend on the number of swaps and the number of flips required to solve the final three edge cubies.
Recall that a single Y-move does two swaps and one flip. Therefore, more than one Y-move may be required to do several flips, and if just one swap is required, we have to do combine the Y-move with additional U-moves.
- Solve the green-orange cubie.
In this example, there is just one Y-move to
do the flip, RUiRiU, and the other two cubies
luckily fall into place.If there are two Y-moves to solve green-orange,
check whether one of them solves it all.If green-orange is in the right position but
flipped, you can solve it with two Y-moves. - Suppose green-orange is solved, but the remaining two cubies are not solved.
There are three cases.
0 swaps and 2 flips.
We need two Y-moves to undo the flips.
Start with Y down the front edge,
finish with Yi sideways to the right.1 swap and 0 flips.
Denoting the sideways Y-move to the left
with X = UFiUiF, we do U X U X U.Doing a Y-move with the swapped cubies
orange-yellow and green-yellow does not help.
However, we can swap blue-yellow next to
orange-yellow, and then swap red-yellow
next to blue-yellow, and the remaining
cubies fall into place.1 swap and 2 flips.
We undo the flips and swap separately as shown
in the previous cases. Order doesn't matter.
Comments
The basic issue solving the last edge cubies is that a Y-move corresponds to two swaps of edge cubies. Several Y-moves will therefore do an even number of swaps. If our scrambled cube happens to require an odd number of edgie swaps, then we can solve most edge cubies with Y-moves, but a single swap remains to be done in the end. However, since a single U amounts to three swaps, which is an odd number, we can find a solution involving an odd number of U-moves.
As it turns out, there are four simple moves based on U and Y (sideways) that can swap the last two cubies. Those are UXUXU, UZUZU, UiXiUiXiUi, UiZiUiZiUi. That is, we don't even have to remember the direction of the U-moves or the sideways Y-moves.
Alternatives
We motivate UXUXU et al. by noting that a Y-move involving the two swapped cubies apparently does not help, so we throw in some U-moves and operate on orange-yellow and green-yellow separately.
Actually, I find an alternative viewpoint based on counting swaps easier to remember and more satisfying as well. Let's take the observation that 1 Y-move does 2 swaps to heart.
If we notice that to solve the final edge cubies requires an odd number of swaps, then we know right away that our 2-swap Y-move cannot do it by itself. However, we also know that a single U does 3 swaps. Therefore, faced with a cube that requires an odd number of edge-cubie swaps, we can do a single U turn to obtain a cube requiring an even number of swaps.
This fits well to our standard strategy of prepare, Y-move, restore. If we prepare with U and restore with Ui, this does not change the number of swaps. Doing any number of U-moves and restoring with their inverses does not change the number of swaps.
Being aware of the swap count therefore suggests the following alternative strategy for solving the last 5 edge cubies. Before you get started, count the number of swaps required. If the number is even, do nothing. If the number is odd, do a single U turn. Then solve the cube with U-prepare, Y-moves, U-restore, taking care that there always is an even number of U moves, which in fact is our default strategy.
The single-U swap-adjustment strategy actually works, since the laws of the cube 'preserve' the swap count. Once the cube is in a state requiring an even number of edgie swaps, we can solve it with an even number of U-moves and some arbitrary number of Y-moves.
Alternatives - Examples
First of all, we can understand how UXUXU works from the point of view of swap counting. In the example above:
|
1 swap and 0 flips. |
In practice, we may want to do that single-U swap-adjustment earlier, say after solving just 1 or 2 of the last 5 edge cubies. The closer we are to solving all 5, the easier it is to count the swaps. Ignoring the swap count may mean that we solve edgies that we have to redo in the end. If we adjust the swap count early, we will never encounter the 1 swap with 0 (or 2) flips configuration.
Here is an example:
| Initially, we count two swaps. Red-yellow and orange-yellow are in the solved position (ignoring orientation). The other three could be positioned correctly with two swaps: green-yellow with blue-yellow, then blue-yellow with green-orange. | ||||||
|
Ignoring swaps. | ||||||
|
Notice that there are 2 swaps initially. | ||||||
|
Adjust swaps after solving one cubie. |
Alternatives - Conclusion
In conclusion, to fully appreciate the Y-move, we want to be aware of its 2-swap property. However, if you find this entire swap-count business confusing (or, like me, sometimes make mistakes in counting the swaps), don't worry. Just solve until only one or zero edge swaps remain. If you need one swap, just do a single U-turn and solve again. Elegantly with UXUXU if you remember, or just start over and solve with the standard Y-move strategy.