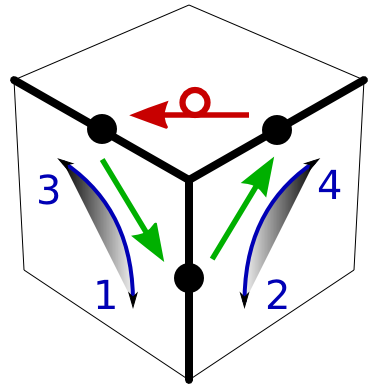
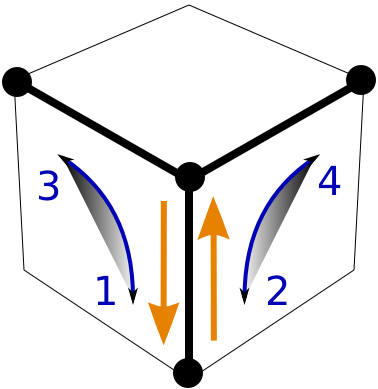
A Beginner's Method
to Solve The Cube
Basics
Solving the Cube
- Step 1: Bottom Edges
- Step 2: Bottom Corners
- Step 3: Middle Edges
- Step 4: Top Edges
- Step 5: Solve Edges
- Step 6: Position Corners
- Step 7: Solve Corners
- Done
Extras
Notation
Some Notation and Technical Terms
We use some pretty standard terminology, which we summarize here.
- Our cube is made of 26 small cubies. The cube is solved when the colors on the 8 corner cubies and the 12 edge cubies match the color of the central cubies. We also call a single cubie solved if it is in the right position with the right orientation as required for solving the big cube.
- The cubies are moved relative to each other by turning one of the layers of the cubes by 90 degrees while holding the other two layers fixed. We call such a quarter-turn an elementary move or basic move.
- We denote face turns by F (front), R (right), L (left), B (back), U (up), and D (down). These are clockwise when looking down on the face. For the counter-clockwise, inverse move we write Fi etc.
- If we rotate the entire cube and not just one face, we write rF, rFi etc. Although the cube did not change, an elementary move like R can now affect a different face.
- Doing the move F twice can be written as F F = F2 or 2*F. For elementary moves, 2*F = 2*Fi, 3*F = Fi, 4*F = I, the identity.
- A sequence of moves written like F R U means to first turn F, then R, then U. Its inverse is Ui Ri Fi. We have to reverse the order so that FRU UiRiFi is the identity.
A little more technical but also useful:
- Given two moves A and B, we call A B Ai a conjugate move. Do A, then B, then do A in reverse. A conjugate is a typical prepare, work, restore operation. There also is B A Bi, which in general is a different conjugate.
- Given two moves A and B, we call A B Ai Bi a commutator move. We do A B, then Ai Bi, but note that Ai Bi is not the inverse (which would be Bi Ai). Basically, we undo A B except those pieces where the order of moves matters. The Y-move defined below corresponds to the elementary commutator A Bi Ai B.
- Conjugates and commutators have some nice properties, in particular they tend to localize/minimize the "side-effects" of moves.