Further Thoughts

Review of the LBL-Y method

The LBL-Y method is a layer-by-layer method with a spare column (like Wikibook-2008, 8355, or SAM), with the special feature that quite some thinking went into how to implement the basic strategy with essentially only one basic move sequence, the Y = FRiFiR move.

Having gone through the method step by step, let us review the LBL-Y method as a Y-move-only approach.

  • FRiFiR fits beautifully into the layer-by-layer-with-spare-column method.
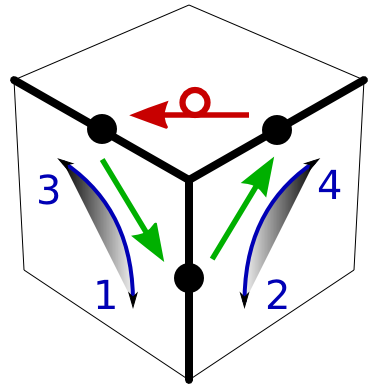
    FRiFiR affects three edges attached to one corner. Two edges are in one layer, say the U-layer, but for things to remain simple, it is very convenient to have a spare vertical column available for the third edge. This is particularly helpful in step 3, 5, and 6 of our method. FRiFiR does not necessarily play a similarly natural role in other strategies.

  • FRiFiR is in some respect the simplest sequence with useful effects and minimal side effects.
    It is simple because only two elementary moves F and R are involved, and there are only four moves total. It has few side effects because only four corners and three edges are involved. (In some sense it is a "local minimum": adding more moves increases the side effects before things become simpler again.) And FRiFiR nevertheless produces useful, non-trivial effects.

  • FRiFiR is well motivated.
    FRiFiR is not something strange or surprising. It happens to be the simplest commutator of two elementary moves. There are only two types of basic two move sequences that overlap at one edge: FR and FRi. For minimal side effects consider the commutators, FRFiRi and FRiFiR. You may think that you need more complicated moves, say more than 4 elementary moves, or sequences involving a third face, say something built from FRU. However, it turns out that already FRiFiR is a rather universal tool. It can serve as swiss army pocket knife.

  • FRiFiR or FRFiRi, your choice.
    There are two elementary commutators, and both accomplish essentially the same things. Conrad Rider's SAM (and 8355 in parts) rely on FRFiRi, which affects three connected edges in the shape of a "Z" rather than a "Y". In a minor way, the Y-move may be somewhat easier to visualize for beginners, but much more important is that in contrast to most other methods SAM and LBL-Y rely on only one move.

  • FRiFiR plays the role of a swiss-army pocket knife.
    FRiFiR swaps and rotates corners, and it cycles and flips edges. Whether simple or not, we are looking for moves that achieve something simple. FRiFiR qualifies as a good tool because we can focus on a basic task like "move edge with a flip", or "swap two corners", and we do not have to worry (much) about side effects. FRiFiR is a pocket knife and not a sword or an axe in the sense that there are more complicated moves that achieve the same effect with fewer side effects, or that achieve more complicated goals. However, more powerful tools are also harder to wield.

  • FRiFiR's effect can be remembered by the effect of the first move.
    In order to apply FRiFiR efficiently, you have to remember details like whether the edge cycle is clockwise or counter-clockwise. In many cases the first quarter-turn determines the overall outcome. If you want a counter-clockwise cycle, start with F because F sends the up-front edge cubie one step along a counter-clockwise circle. If you want the up-front-right corner cubie swapped down, either F or Ri as first move accomplish that. However, only F rotates this corner cubie simultaneously such that the front sticker remains on the front side. Call this the "greedy" strategy: do a single turn first that does what you want, then finish with the remainder of the Y-move that fits your first move.

  • FRiFiR plus elementary moves are needed.
    We need moves that are general enough to unscramble the cube. Clearly, FRiFiR is not general enough by itself, even if done in all possible places and with all possible orientations. However, the remaining work happens very unobtrusively in elementary moves, like turning the U-layer in preparation of some Y-move sequence.

  • FRiFiR does all the hard work - almost.
    As just stated, with Y-moves and some elementary prepare/restore moves we can solve the cube. I would say that this is not clear a priori. In fact, we do encounter a potentially serious stumbling block at the end of Step 4/5, where we need a single swap but Y only does swaps in pairs. In a sense, Y-moves do all the heavy lifting, but when faced with a single swap it is the humble U move that fixes it. It is neat that understanding the even-swap property of the Y-move solves the problem. Other solutions like the Wikibook-2008 solution or the 8355 method simply introduce a new, special move to solve that case. There is a specific Y-move sequence, UXUXU, that we could use, so yes, we can do it with Y-moves and U-moves. On the other hand, we don't have to memorize UXUXU. All we have to remember is that Y does an even number and U does an odd number of swaps.

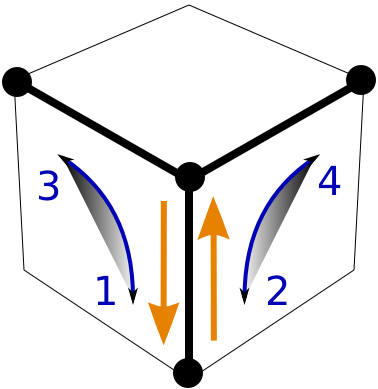
  • If you have mastered FRiFiR, you get FRiFi for free.
    FRiFi is a three-move, elementary conjugate. Turn one face (F) to set up a move (Ri), then undo your preparations (Fi). This is so simple that it can be justifiably called "intuitive" once you are beyond the beginning stages. You can also call it a FRiFiR where the final R is not needed (or not wanted). This typically happens when there is a layer that can be freely turned, like the U-layer in our strategy during step 1, 2, and 3.

  • Only one move needs to be memorized.
    The promise of the method is that you only have to teach yourself one sequence, and it is short and simple. On the other hand, who says that it is no fun to memorize moves? To have an amazing bag of tricks at your disposal? There are moves where you only have to push a mental button and three corners are cycled, five edges flipped, and your plants are watered. With a larger bag of tricks you can certainly solve the cube in less moves, and it is a great mental exercise. So if you tire of Y-moves, by all means, look at more challenging, more efficient, perhaps more elegant methods. Although getting by with only one move is a neat challenge in itself.